Bayes
Einleitung
Wie funktioniert MCMC?
Betrachten wir zuerst den Ausgangspunkt unserer weiteren Betrachtungen, die Bayes Formel:
\[ P( \vec{\theta} | \vec{x}) = \frac{ P( \vec{x} | \vec{\theta}) \cdot P( \vec{\theta})} {P(\vec{x})}\]
Der Ausdruck \(P(\vec{\theta}│\vec{x})\) beschreibt die Wahrscheinlichkeit für die Modellparameter \(\vec{\theta}\), wenn die Daten \(\vec{x}\) gegebenen sind und wird als Posterior bezeichnet.
In den meisten Anwendungsfällen sind wir mit der folgenden Fragestellung konfrontiert: Wir haben ein Modell oder eine Hypothese, welche durch die Parameter \(\vec{\theta}\) beschrieben werden kann. Diese sind in der Regel unbekannt. Und wir haben die Daten \(\vec{x}\), die in den meisten Fällen durch eine oder mehrere Messungen bestimmt wurden.
Die Bayes Formel zeigt einen Weg auf, wie die Wahrscheinlichkeitsverteilung \(P( \vec{\theta} | \vec{x}) \) aus anderen Wahrscheinlichkeitsverteilungen ermittelt werden kann.
Hier ist zum einen die sogenannte Likelihood \(P( \vec{x} | \vec{\theta})\). Diese beschreibt die Wahrscheinlichkeitsverteilung für das Modell oder die Hypothese (mit den zu bestimmenden Parametern \(\vec{\theta} \), von den wir annehmen, dass sie die Verteilung der Daten \( \vec{x} \) am besten beschreiben.
Der Prior \( P(\vec{\theta}) \) beschreibt die Wahrscheinlichkeitsverteilung für unsere Annahmen zu den einzelnen Parametern \( \vec{\theta} \), die wir ohne Kenntnis der (neuen) Daten \( \vec{x} \) haben. Der Prior gibt also unser Vorwissen oder unsere Vermutungen über die Parameter wieder. Likelihood und Prior werden miteinander multipliziert und bilden den Zähler der Bayes Formel.
Der Ausdruck im Nenner, die sogenannte Evidence \( P(\vec{x}) \), beschreibt die Wahrscheinlichkeit, dass die Daten \( \vec{x} \) durch unser gewähltes Modell oder unsere Hypothese beschrieben werden. Diese kann prinzipiell durch Integration über alle möglichen Parameterwerte \( \vec{\theta} \) berechnet werden.
\[ P( \vec{x}) = \int \limits_{\vec{\theta}} P(\vec{x} | \vec{\theta}) \cdot d\vec{\theta} \]
Wie schon geschrieben, sie kann auf diese Art prinzipiell berechnet werden. Selbst für einfachste Modelle lässt sich das Integral in der Regel nicht in einer geschlossenen Form berechnen.
Ein geeigneter Ansatz um dieses Problem anzugehen ist der Einsatz von Markov Chain Monte Carlo (MCMC) Algorithmen. Diese basieren auf der Erstellung einer Markov Kette, die dann für Monte Carlo Approximationen verwendet wird). Dies klingt auf den ersten Blick recht kompliziert. Dass dem nicht so ist – zumindest für einfache Anwendungen – wollen wir an einigen Beispielen zeigen.
Posterior für normalverteilte Daten
Beginnen wir mit einem einfachen Beispiel. Gegeben seien Messdaten, von denen wir wissen, dass sie normalverteilt um den Wert 0 sind. Die Standardabweichung der Normalverteilung sei 1.
Der nachfolgende Python-Code (zur Nutzung in einem Jupyter-Notebook) simuliert unsere Messdaten.
# package provides support for matplotlib to display figures directly inline in the Jupyter notebook
%matplotlib inline
# import modules
import numpy as np
import scipy as sp
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from scipy.stats import norm
sns.set_style('whitegrid') # control the general style of the plots: dict, or one of {darkgrid, whitegrid, dark, white, ticks}
sns.set_context('notebook') # control the scaling of plot elements: dict, or one of {paper, notebook, talk, poster}
np.random.seed(123) # initialize the random number generator
numdata = 25 # number of datapoints
data = np.random.randn(numdata)
ax = plt.subplot()
sns.histplot(data, kde=False, ax=ax) == ax.set(title='Histogram of observed data', xlabel='interval', ylabel='# observations');
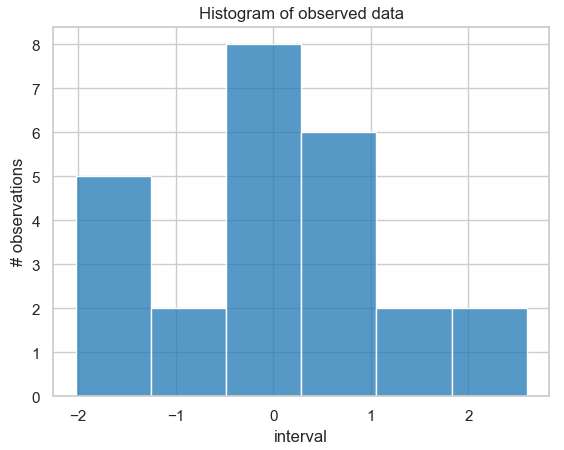
Histogramm der Häufigkeitsverteilung von 25 simulierten Messdaten, die um den Wert 0 normalverteilt sind mit Standardabweichung 1.
Da wir wissen, dass wir für die Simulation eine Normalverteilung mit Mittelwert \(\mu=0\) und Standardabweichung 1 verwendet haben, können wir uns die gesuchte Lösung in diesem Ausnahmefall auch analytisch bestimmen und später für Vergleichszwecke nutzen. Der Grund hierfür ist, dass für eine normalverteilte Likelihood mit bekannter Standardabweichung der normalverteilte Prior konjugiert ist (d. h. die Posterior hat die gleiche Verteilung wie der Prior). Somit wissen wir, dass der Posterior mit Mittelwert \(\mu\) ebenfalls normalverteilt ist.
Hier noch der Python-Code zur Berechnung der analytischen Lösung:
# function for calculating posterior analytically
def calc_posterior_analytical(data, x, mu_0, sigma_0):
sigma = 1. # standard deviation is fixed!
n = len(data) # number of data
mu_post = (mu_0 / sigma_0**2 + data.sum() / sigma**2) / (1. / sigma_0**2 + n / sigma**2)
sigma_post = (1. / sigma_0**2 + n / sigma**2)**-1
return norm(mu_post, np.sqrt(sigma_post)).pdf(x)
ax = plt.subplot()
x = np.linspace(-1, 1, 500)
posterior_analytical = calc_posterior_analytical(data, x, 0., 1.)
ax.plot(x, posterior_analytical)
ax.set(xlabel='mu', ylabel='belief', title='Analytical posterior');
sns.despine()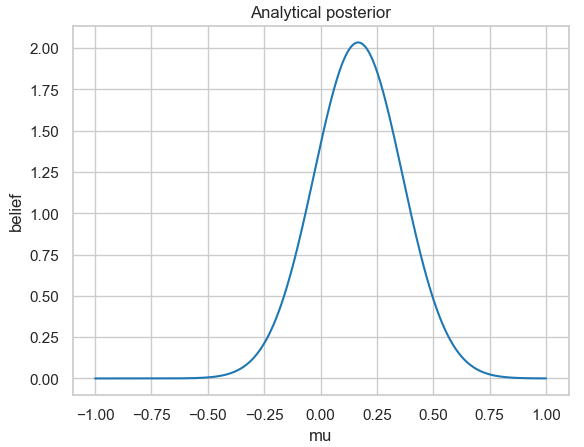
Analytisch berechnete Posterior-Wahrscheinlichkeitsverteilung für die 25 simulierten normalverteilten Messdaten mit fester Standardabweichung 1.
Wenn Sie sich die Abbildung genau ansehen, dann werden Sie feststellen, dass für die analytische Lösung die Posterior-Verteilung den Mittelwert nicht bei \(\mu = 0\) hat. Dies liegt daran, dass wir nur eine geringe Anzahl an Messdaten zufallsverteilt aus einer Normalverteilung bestimmt hatten.
Zur Vertiefung:
Lassen Sie den Code doch mal mit höheren Werten für die Anzahl an simulierten Messdaten in einem Jupyter Notebook laufen und beobachten Sie, wie sich die analytische Lösung verhält.
Nach diesen vorbereitenden Schritten wollen wir uns jetzt unserer eigentlichen Aufgabe zuwenden: wir wollen die Posterior-Verteilung \( P(\vec{\theta} | \vec{x}) \) aus der Bayes-Formel bestimmen. Gegeben haben wir bereits die oben simulierten Messdaten \( \vec{x} \).
Als nächstes benötigen wir die Likelihood-Funktion \( P( \vec{x} | \vec{\theta}) \). Für unser einfaches Beispiel nehmen wir an, dass das Modell eine Normalverteilung ist.
Gut, Sie werden natürlich jetzt sagen, das ist ja logisch, da wir unsere Messdaten aus einer Normalverteilung simuliert haben. Also warum sollten wir jetzt ein anderes Modell verwenden? Das stimmt! Aber die Simulation haben wir nur genutzt, um Messdaten zu erzeugen. Jetzt „vergessen“ wir einfach einmal wie wir die sie erzeugt haben. Unsere Ausgangspunkte (Annahmen) für die nächsten Schritte sind dann:
- Wir haben eine Anzahl an n Messdaten
- Jeder Messwert ist dem Ausgangswert (in diesem Fall dem Wert der Normalverteilung) gleich, d. h. es müssen keine zusätzlichen Eigenschaften, wie Detektoreffizienzen oder Abstandsabhängigkeiten etc. berücksichtigt werden (hierzu später mehr).
- Wir unterstellen als Modell eine Normalverteilung (wir könnten auch eine andere Verteilung annehmen, z. B. eine Poisson-Verteilung, eine Student-Verteilung etc. Wenn wir uns aber die Häufigkeitsverteilung ansehen, dann könnte es eben auch eine Normalverteilung sein. Was passiert, wenn wir ein „falsches“ Modell wählen, darum werden wir uns später kümmern).
Hieraus folgt, dass auch die Likelihood-Funktion eine Normalverteilung ist! Diese hat zwei Parameter, den Mittelwert \(\mu\) und die Standardabweichung \(\sigma\), die wir in unserem Beispiel gleich 1 setzen.
Unser Ziel ist es, den Posterior \( P(\vec{\mu} | \vec{x}) \) zu bestimmen, mit \((\vec{\mu} = \mu) \), da wir nur einen Parameter in unserem Model haben, den Mittelwert \(\mu\) (\(\sigma\) hat ja einen festen Wert). Wir können das Modell in mathematischer Schreibweise wie folgt schreiben:
\[ \mu \sim ( \vec{x} | \mu, 1) \]
Jetzt haben wir aber immer noch das Problem, dass wir die Evidence \( P(\vec{x}) \) nicht kennen und im Normalfall auch nicht analytisch berechnen können. Hier kommt nun das MCMC sampling, das Markov Chain Monte Carlo Stichprobenverfahren, ins Spiel. Durch seine Anwendung müssen wir das Integral gar nicht berechnen!
Der „Trick“ besteht einfach darin, dass der Algorithmus nicht direkt den Posterior berechnet, sondern das Verhältnis zwischen dem normalisierten und dem nicht-normalisierten Posteriors verwendet.
Die Evidence ist ja für die Normalisierung der Lösung, dem Posterior, verantwortlich. Das Integral wird für die gegebenen Messwerte \(\vec{x}\) für alle Werte von \(\mu\) bestimmt, d. h. der Wert des Integrals wird nicht davon beeinflusst, welches \(\mu\) gerade in der Bayes-Formel verwendet wird.
In unserem Beispiel mit dem (einzigen) Parameter \(\mu\) setzen wir hierfür die beiden Posteriors
\[ P( \mu | \vec{x}) = \frac{ P( \vec{x} | \mu ) \cdot P( \mu )} {P(\vec{x})}\]
und
\[ P( \mu_0 | \vec{x}) = \frac{ P( \vec{x} | \mu_0 ) \cdot P( \mu_0 )} {P(\vec{x})}\]
zueinander ins Verhältnis
\[ \frac { \frac{ P( \vec{x} | \mu ) \cdot P( \mu )} {P(\vec{x})} }
{ \frac{ P( \vec{x} | \mu_0 ) \cdot P( \mu_0 )} {P(\vec{x})} } =
\frac{ P( \vec{x} | \mu ) \cdot P( \mu ) }
{ P( \vec{x} | \mu_0 ) \cdot P( \mu_0 )} \]
Dann kürzt sich \(P(\vec{x})\) heraus (für den Ausdruck des normalisierten Posteriors haben wir \(\mu_0\) gesetzt, für den nicht-normalisierten \(\mu\))!
Wie wird dies nun alles im MCMC-Algorithmus (unter Verwendung des Metroplois samplers) umgesetzt?
Wir beginnen mit einem willkürlichen Startwert für unsere gesuchte Größe, den Mittelwert \(\mu\).
mu_current = 1. # starting parameter - can be randomly choosenBeachte, dass diese Normalverteilung nichts mit den Normalverteilungen zu tun hat, die wir für die Erzeugung der Messdaten oder unser Modell verwendet haben. Sie wird im Metropolis sampler zur Erzeugung des nächsten \(\mu\)-Wertes verwendet. Dieser wird aus der Normalverteilung „gesampelt“, d. h. zufallsgeneriert ausgewählt.
# new µ-value sampled from normal distribution with fixed standard deviation
mu_proposal = norm(mu_current, proposal_width).rvs() Für diesen neuen (mu_proposal) und den alten (mu_current) \(\mu\)-Wert werden dann die beiden zugehörigen Verteilungen der Likelihoods und der Priors berechnet. Beachte, dass in die Berechnung des Priors der jeweils zugehörige \(\mu\)-Wert eingeht, d. h., wenn ein neuer \(\mu\)-Wert bestimmt wurde, dann ist dieser für die Bestimmung des zugehörigen Priors zu verwenden.
Zuletzt werden die Wahrscheinlichkeitsverteilungen des Zählers der Bayes Formel bestimmt
# for “old” and “new” mu-value calculate …
# … likelihoods
likelihood_current = norm(mu_current, 1).pdf(data).prod()
likelihood_proposal = norm(mu_proposal, 1).pdf(data).prod()
# … prior probabilities
prior_current = norm(mu_prior_mu, mu_prior_sd).pdf(mu_current)
prior_proposal = norm(mu_prior_mu, mu_prior_sd).pdf(mu_proposal)
# ….nominator of Bayes formula
p_current = likelihood_current * prior_current
p_proposal = likelihood_proposal * prior_proposalWird dieses Stück Code wiederholt ausgeführt, dann handelt es sich um einen einfachen Hill-Climbing-Algorithmus. Nach jedem Durchlauf wird der neue \(\mu\)-Wert zum alten \(\mu\)-Wert und mit diesem ein neuer \(\mu\)-Wert gesampelt, für den die Wahrscheinlichkeitsverteilung des neuen Zählers der Bayes Formel bestimmt wird (der neue Wert aus dem vorherigen Durchlauf wird zum neuen alten Wert). Hierbei sind Änderungen des \(\mu\)-Wert in beiden Richtungen möglich, (der neue Wert kann größer oder kleiner als der vorherige Wert sein). Da wir aber aus einer Normalverteilung die jeweils neuen Werte „sampeln“, wird sich über lange Sicht der Wert dem Wert \(\mu = 0 \) annähern.
Allerdings sind wir nicht nur an dem endgültigen Mittelwert von \(\mu\) interessiert, sondern wir wollen auch dessen Wahrscheinlichkeitsverteilung bestimmen. Und hier setzt der eigentliche „Trick“ des MCMC an: Wir bestimmen eine Akzeptanz-Wahrscheinlichkeit aus den beiden Zähler-Wahrscheinlichkeiten
p_accept = p_proposal / p_current # acceptance probabilityund unterscheiden zwei Fälle: wenn die Akzeptanz-Wahrscheinlichkeit
- größer als 1 ist, dann wird der neue \(\mu\)-Wert akzeptiert
- kleiner als 1 ist, dann wird der neue \(\mu\)-Wert mit einer durch die Akzeptanz-Wahrscheinlichkeit bestimmten Wahrscheinlichkeit akzeptiert.
Und das ist der gesamte MCMC-Algorithmus! Verblüffend einfach für etwas, das auf den ersten Blick extrem kompliziert aussieht, oder?
Anmerkung:
Warum haben wir dieses Beispiel gewählt? Die Antwort ist relativ einfach. Der Prior ist eine Normalverteilung und die Konjugierte einer Normalverteilung ist wieder eine Normalverteilung, d. h. dieses Beispiel kann auch von Hand berechnet werden, was es uns erleichtert, das erzielte Ergebnis zu verifizieren.
Zum Abschluss nochmals der gesamte Python-Code zum selber ausprobieren (er wurde, wie auch der überwiegende Teil der voranstehenden Beschreibung aus dem hervorragenden Blog von Thomas Wiecki entnommen).
def sampler(data, samples=4, mu_init=.5, proposal_width=.5, plot=False, mu_prior_mu=0, mu_prior_sd=1.):
mu_current = mu_init
posterior = [mu_current]
for i in range(samples):
# suggest new position
mu_proposal = norm(mu_current, proposal_width).rvs()
# Compute likelihood by multiplying probabilities of each data point
likelihood_current = norm(mu_current, 1).pdf(data).prod()
likelihood_proposal = norm(mu_proposal, 1).pdf(data).prod()
# Compute prior probability of current and proposed mu
prior_current = norm(mu_prior_mu, mu_prior_sd).pdf(mu_current)
prior_proposal = norm(mu_prior_mu, mu_prior_sd).pdf(mu_proposal)
p_current = likelihood_current * prior_current
p_proposal = likelihood_proposal * prior_proposal
# Accept proposal?
p_accept = p_proposal / p_current
# Usually would include prior probability, which we neglect here for simplicity
accept = np.random.rand() < p_accept
if plot:
plot_proposal(mu_current, mu_proposal, mu_prior_mu, mu_prior_sd, data, accept, posterior, i)
if accept:
# Update position
mu_current = mu_proposal
posterior.append(mu_current)
return np.array(posterior)
# Function to display
def plot_proposal(mu_current, mu_proposal, mu_prior_mu, mu_prior_sd, data, accepted, trace, i):
from copy import copy
trace = copy(trace)
fig, (ax1, ax2, ax3, ax4) = plt.subplots(ncols=4, figsize=(16, 4))
fig.suptitle('Iteration %i' % (i + 1))
x = np.linspace(-3, 3, 5000)
color = 'g' if accepted else 'r'
# Plot prior
prior_current = norm(mu_prior_mu, mu_prior_sd).pdf(mu_current)
prior_proposal = norm(mu_prior_mu, mu_prior_sd).pdf(mu_proposal)
prior = norm(mu_prior_mu, mu_prior_sd).pdf(x)
ax1.plot(x, prior)
ax1.plot([mu_current] * 2, [0, prior_current], marker='o', color='b')
ax1.plot([mu_proposal] * 2, [0, prior_proposal], marker='o', color=color)
ax1.annotate("", xy=(mu_proposal, 0.2), xytext=(mu_current, 0.2),
arrowprops=dict(arrowstyle="->", lw=2.))
ax1.set(ylabel='Probability Density', title='current: prior(mu=%.2f) = %.2f\nproposal: prior(mu=%.2f) = %.2f' % (mu_current, pri-or_current, mu_proposal, prior_proposal))
# Likelihood
likelihood_current = norm(mu_current, 1).pdf(data).prod()
likelihood_proposal = norm(mu_proposal, 1).pdf(data).prod()
y = norm(loc=mu_proposal, scale=1).pdf(x)
sns.distplot(data, kde=False, norm_hist=True, ax=ax2)
ax2.plot(x, y, color=color)
ax2.axvline(mu_current, color='b', linestyle='--', label='mu_current')
ax2.axvline(mu_proposal, color=color, linestyle='--', label='mu_proposal')
#ax2.title('Proposal {}'.format('accepted' if accepted else 'rejected'))
ax2.annotate("", xy=(mu_proposal, 0.2), xytext=(mu_current, 0.2),
arrowprops=dict(arrowstyle="->", lw=2.))
ax2.set(title='likelihood(mu=%.2f) = %.2f\nlikelihood(mu=%.2f) = %.2f' % (mu_current, 1e14*likelihood_current, mu_proposal, 1e14*likelihood_proposal))
# Posterior
posterior_analytical = calc_posterior_analytical(data, x, mu_prior_mu, mu_prior_sd)
ax3.plot(x, posterior_analytical)
posterior_current = calc_posterior_analytical(data, mu_current, mu_prior_mu, mu_prior_sd)
posterior_proposal = calc_posterior_analytical(data, mu_proposal, mu_prior_mu, mu_prior_sd)
ax3.plot([mu_current] * 2, [0, posterior_current], marker='o', color='b')
ax3.plot([mu_proposal] * 2, [0, posterior_proposal], marker='o', color=color)
ax3.annotate("", xy=(mu_proposal, 0.2), xytext=(mu_current, 0.2),
arrowprops=dict(arrowstyle="->", lw=2.))
#x3.set(title=r'prior x likelihood \(\propto\) posterior')
ax3.set(title='posterior(mu=%.2f) = %.5f\nposterior(mu=%.2f) = %.5f' % (mu_current, posterior_current, mu_proposal, posteri-or_proposal))
if accepted:
trace.append(mu_proposal)
else:
trace.append(mu_current)
ax4.plot(trace)
ax4.set(xlabel='iteration', ylabel='mu', title='trace')
plt.tight_layout()
#plt.legend()
Zum Starten des Codes benötigen wir noch zwei weitere Zeilen.
np.random.seed(123)
sampler(data, samples=8, mu_init=-1., plot=True);Ein beispielhaftes Ergebnis der Ausführung obigen Codes zeigen die nachfolgenden Abbildungen. Für jeden Iterationsschritt werden (von links nach rechts)
- die Prior-Wahrscheinlichkeitsverteilung (d. h. unsere Vermutung über die Verteilung von \(\mu\) bevor wir die (Mess-)Daten berücksichtigt haben) mit den roten bzw. blauen vertikalen Linien für den aktuellen bzw. vorgeschlagenen neuen \(\mu\)-Wert,
- die Likelihood-Verteilung als grüne oder rote Linie, je nachdem ob der Wert für \(\mu\) akzeptiert wird oder nicht, sowie das Histogramm der verwendeten Daten im Hintergrund,
- die normalisierte Posterior Verteilung und
- die Posterior Samples, die in allen Iterationen bislang bestimmt wurden
für insgesamt acht Iterationsschritte dargestellt.
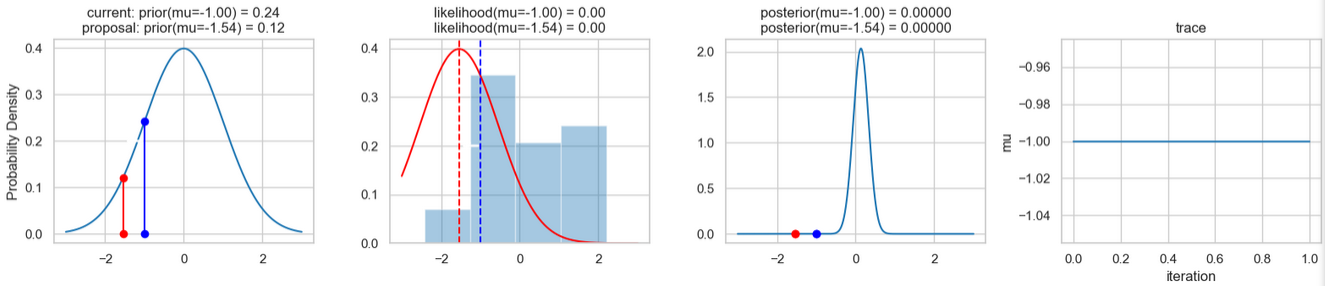
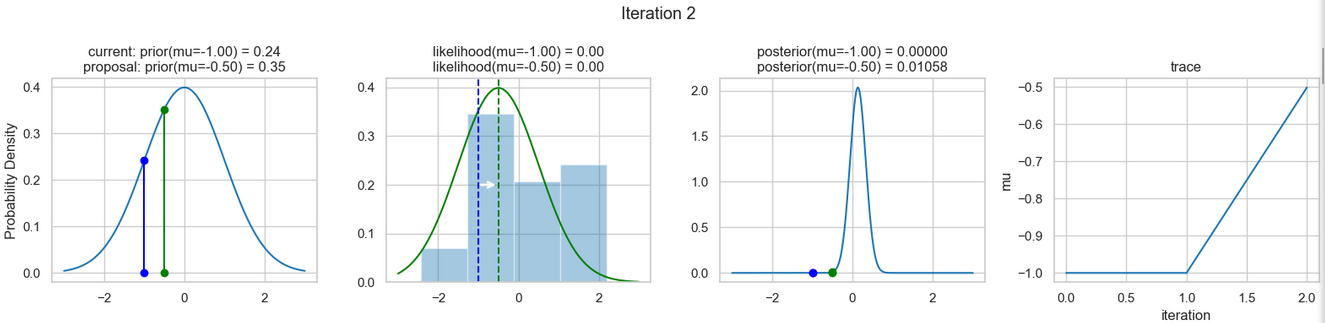
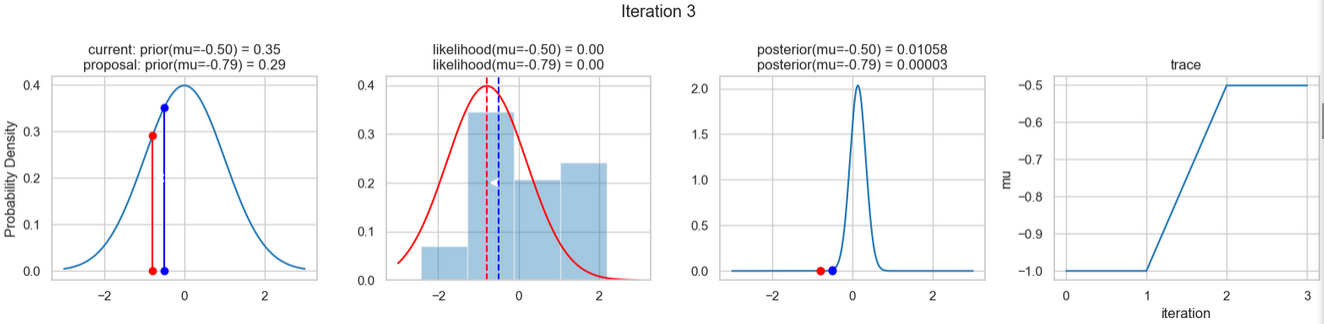
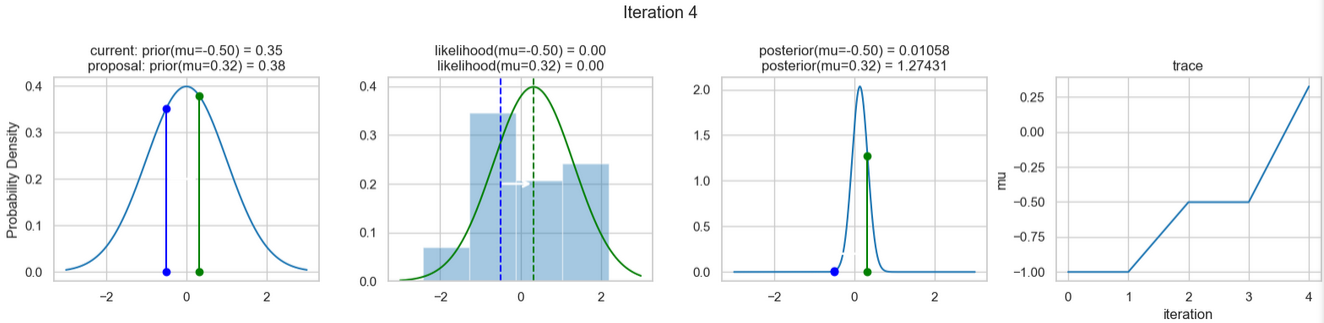
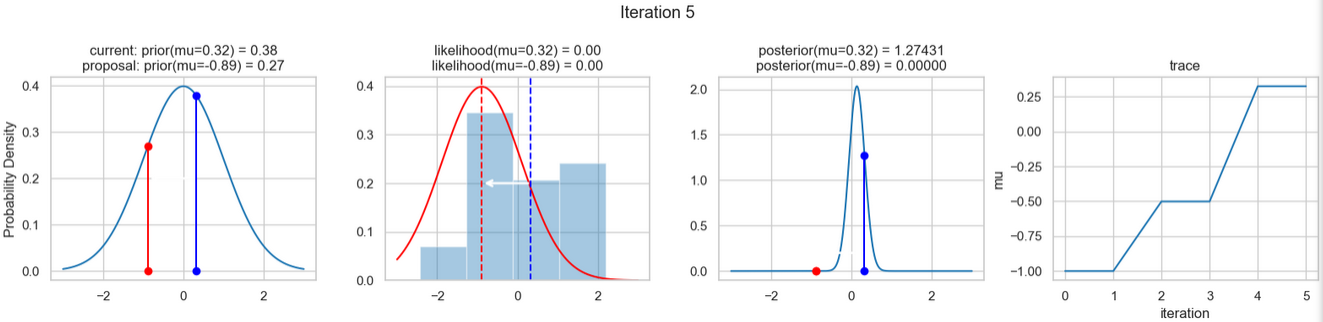
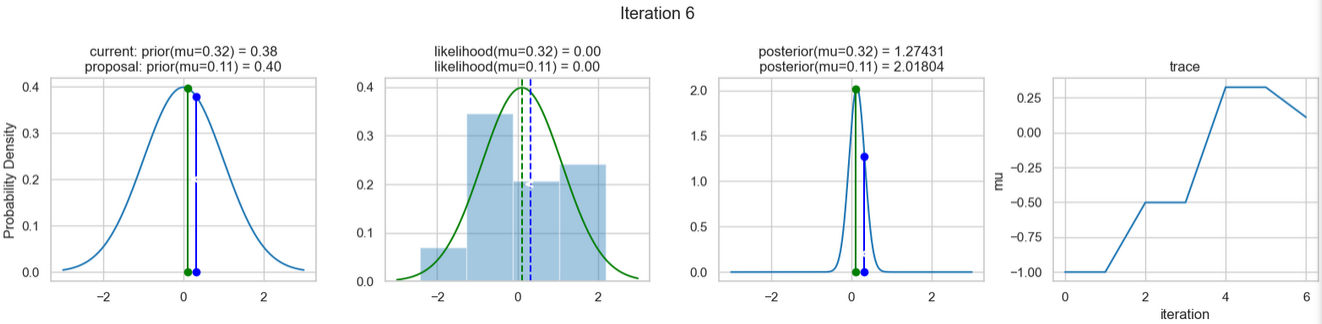
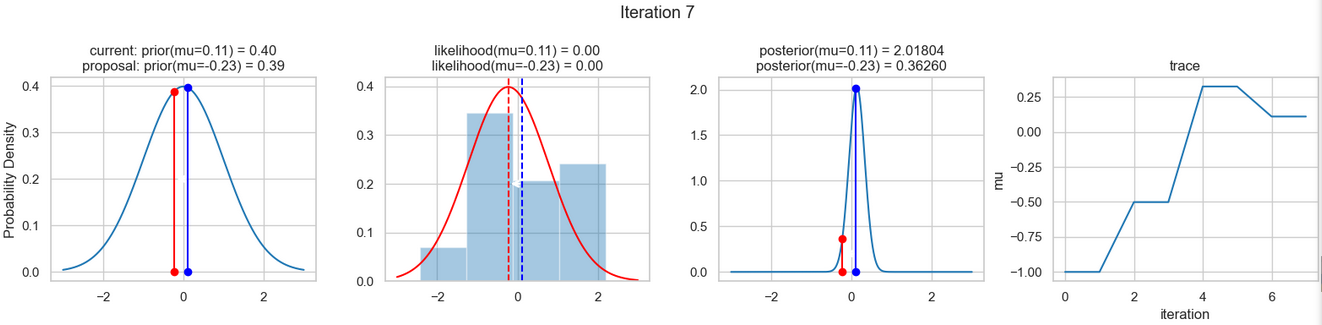
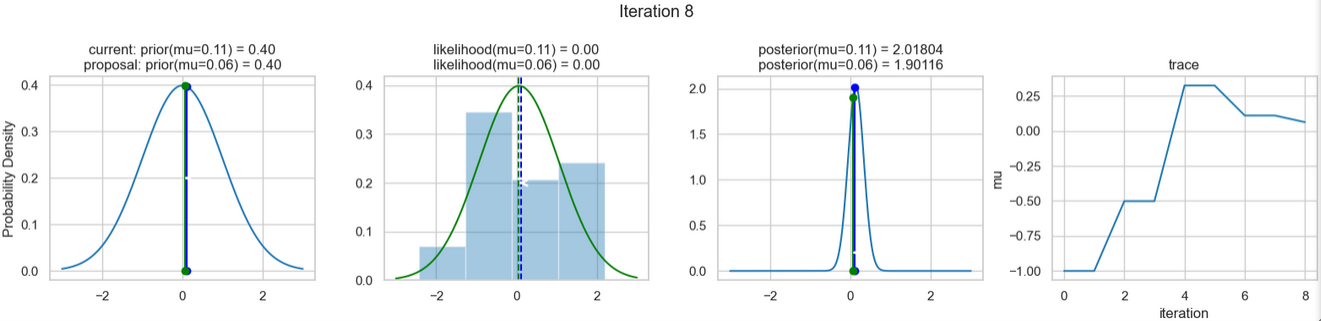
So weit, so gut! Jetzt fehlen uns nur noch einige wenige Schritte, um dieses einfache Beispiel abschließen zu können.
Jede einzelne dieser Iterationen basiert auf der Posterior- Wahrscheinlichkeitsverteilung unseres Modells! Wenn wir nun eine große Anzahl an Iterationen ausführen, dann können wir damit eine Näherung der gesuchten Posterior-Wahrscheinlichkeitsverteilung (d. h. die Anwendung der Bayes Formel) erhalten. Hier der zugehörige Python-Code:
posterior = sampler(data, samples=15000, mu_init=1.)
fig, ax = plt.subplots()
ax.plot(posterior)
_ = ax.set(xlabel='sample', ylabel='mu');
Die Abbildung zeigt das Ergebnis, das als Trace bezeichnet wird, und für 15.000 Samples ausgeführt wurde (wenn Sie es mit Ihrem Rechner nachvollziehen wollen: die Berechnung dauert einige Zeit, also nicht ungeduldige werden).
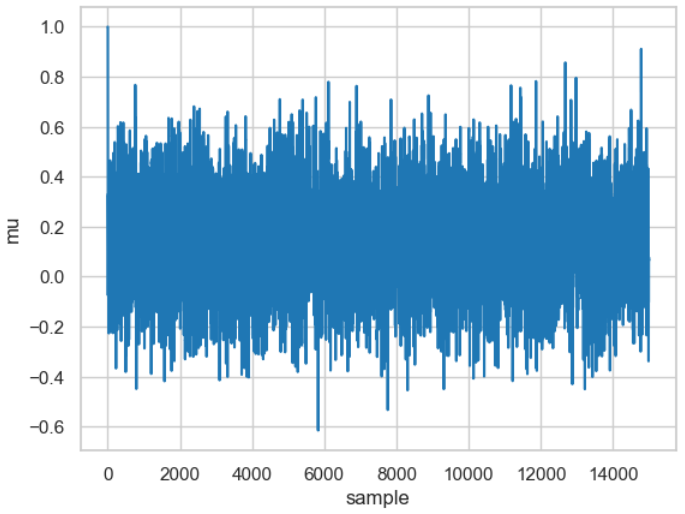
Aus dem Trace kann nun sehr einfach eine Näherung der gesuchten Posterior-Wahrscheinlichkeitsverteilung ermittelt werden indem man das Histogramm dafür erstellt.
Hier der genutzte Code dafür:
ax = plt.subplot()
sns.distplot(posterior[500:], ax=ax, label='estimated posterior')
x = np.linspace(-.5, .5, 500)
post = calc_posterior_analytical(data, x, 0, 1)
ax.plot(x, post, 'g', label='analytic posterior')
_ = ax.set(xlabel='mu', ylabel='belief');
ax.legend();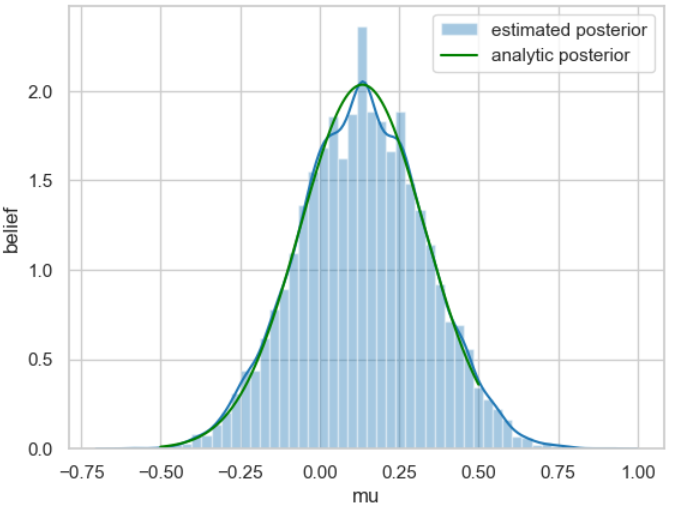
Zum besseren Vergleich ist die am Anfang des Beispiels analytisch berechnete Posterior-Wahrscheinlichkeitsverteilung grün eingezeichnet.
Eigentlich sind wir jetzt fertig. Wir haben ein Verfahren näher angesehen, mit dem wir die Bayes-Formel zur Bestimmung der Wahrscheinlichkeitsverteilung nutzen können. Der Vollständigkeit halber, wollen wir an dieser Stelle noch auf einen weiteren Punkt eingehen: die Wahl der Breite der Normalverteilung, die für das Sampling verwendet wird.
Hier gibt es zwei einander wiedersprechende Tendenzen. Einerseits soll die Breite nicht zu schmal sein, da das Sampling extrem ineffizient wird, da es eine lange Zeit dauert den gesamten Parameterraum zu erkunden. Der Verlauf entspricht dann einem typischen Random-Walk, wie das Ergebnis des nachfolgenden Code-Stücks zeigt.
posterior_small = sampler(data, samples=5000, mu_init=1., proposal_width=.01)
fig, ax = plt.subplots()
ax.plot(posterior_small);
_ = ax.set(xlabel='sample', ylabel='mu');
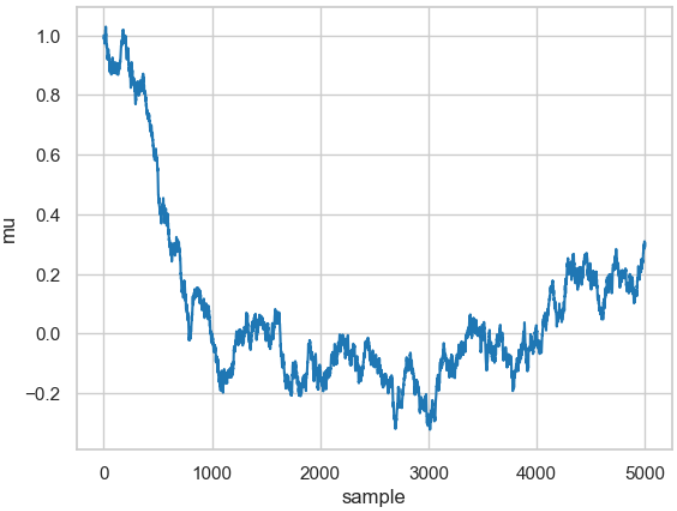
Andererseits kann eine zu breite gewählte Verteilung dazu führen, dass so gut wie keine Iteration zu einem akzeptierten neuen Wert führt, wie beispielsweise mit nachfolgendem Code-Stück gezeigt wird.
posterior_large = sampler(data, samples=5000, mu_init=1., proposal_width=3.)
fig, ax = plt.subplots()
ax.plot(posterior_large); plt.xlabel('sample'); plt.ylabel('mu');
_ = ax.set(xlabel='sample', ylabel='mu');
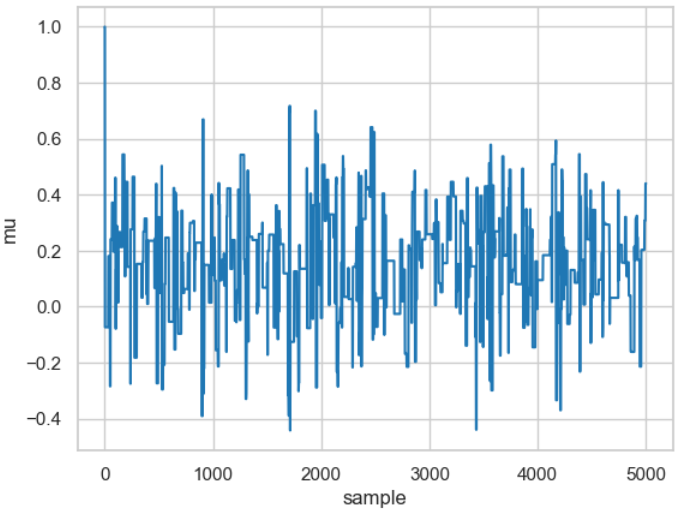
Die Ergebnisse für die beiden Breiten basieren auf derselben Posterior-Wahrscheinlichkeitsverteilung, wie nachfolgend gezeigt.
sns.distplot(posterior_small[1000:], label='Small step size')
sns.distplot(posterior_large[1000:], label='Large step size');
_ = plt.legend();
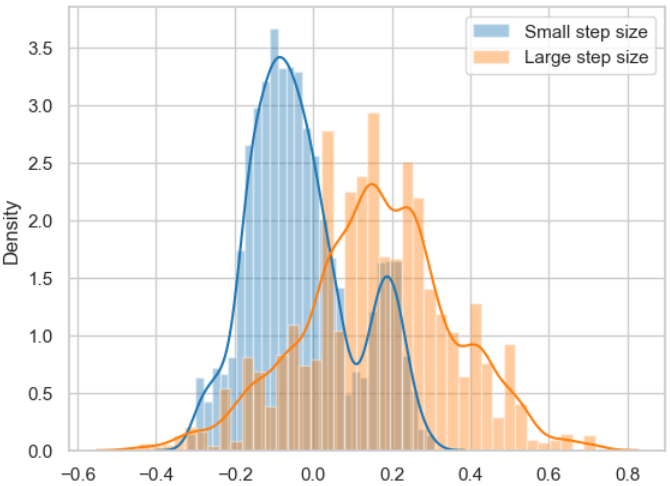
Die Abbildung zeigt deutlich, dass die jeweiligen Samples nicht unabhängig voneinander sind, was aber ein Schlüsselelement für die erfolgreiche Anwendung des MCMC-Algorithmus ist.
Somit stellt sich natürlich die Frage, wie man erkennt, dass die Samples für die gewählten Einstellungen (hier die Standardabweichung der Normalverteilung) voneinander unabhängig und damit effizient sind?
Eine hierfür allgemein verwendete Metrik ist die Autokorrelation, die ermittelt wie korreliert ein Sample mit allen anderen Samples ist.
Auch hierfür ein kleiner Python-Code mit Ergebnisplot:
from pymc3.stats import autocorr
lags = np.arange(1, 100)
fig, ax = plt.subplots()
ax.plot(lags, [autocorr(posterior_large, l) for l in lags], label='large step size')
ax.plot(lags, [autocorr(posterior_small, l) for l in lags], label='small step size')
ax.plot(lags, [autocorr(posterior, l) for l in lags], label='medium step size')
ax.legend(loc=0)
_ = ax.set(xlabel='lag', ylabel='autocorrelation', ylim=(-.1, 1))
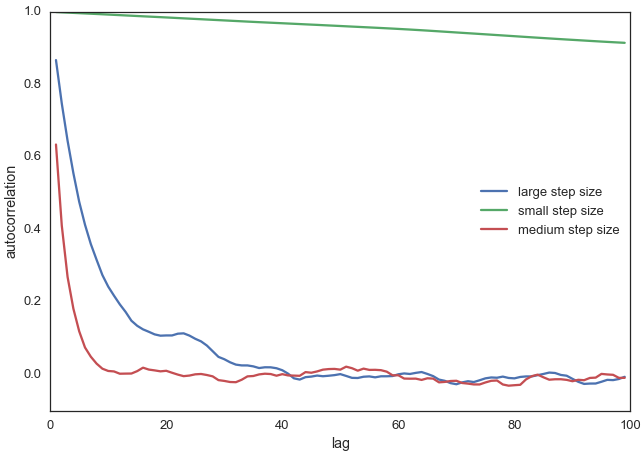
Deutlich erkennt man, dass unsere ursprüngliche Wahl der Breite (\(proposal_width = 0.5\), medium step size, rote Kurve) deutlich weniger Korrelationen aufweist als in den beiden anderen Fällen (grüne und blaue Kurven).
In der Praxis will man die beste Schrittweite automatisch bestimmen lassen, beispielsweise durch das Kriterium, dass ungefähr 50 % der Vorschläge verworfen werden.
Jetzt sind wir aber endgültig am Ende dieses Beispiels angelangt. Wir sollten jetzt ein allgemeines Verständnis für die prinzipielle Anwendung des MCMC-Samplings haben zur Bestimmung der Posterior-Wahrscheinlichkeitsverteilung auf Grundlage vorhandener Messdaten, einem Modell, das der Entstehung der Messdaten zugrunde liegt und vorhandenem a priori Wissen.
Wie erwähnt, es handelt sich hier um ein sehr einfaches Beispiel. Die Praxis erfordert hier deutlich komplexere Schritte – die vorstehenden Grundlagen sind aber meistens unverändert gültig. Und dies wollen wir uns in den nachfolgenden Beispielen etwas näher ansehen.